Chapter 1: Introduction to the Problem

While pondering the intricacies of calculus, a thought emerged: under what circumstances does squaring a function yield its integral?

To determine a function f(x) such that its antiderivative is f(x)², we must consider that integrating a polynomial raises all degrees by one. For instance, the antiderivative of x³ is x⁴/4. This suggests that f(x) should be linear, allowing the x term to integrate into an x² term. We must also identify both the constant term and the coefficient of the x term.

Though this approach is valid, we can streamline the process. We start by differentiating both sides of the equation with respect to x, which conveniently eliminates the integral.

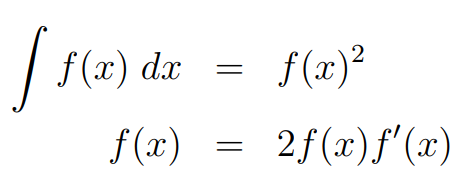
Upon applying the chain rule, we derive the expression on the right side. This leads us to a straightforward differential equation. Observing closely, we can simplify it by canceling f(x) from both sides:

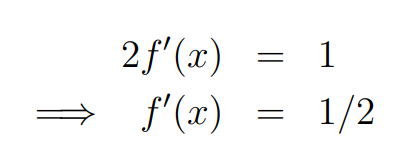
The derivative of f(x) yields 1/2, indicating that f(x) = x/2 + a, where a is a constant. This aligns with our expectation of a linear function. Given that f(x)² must serve as an antiderivative of f(x), we can use this relationship to solve for a.

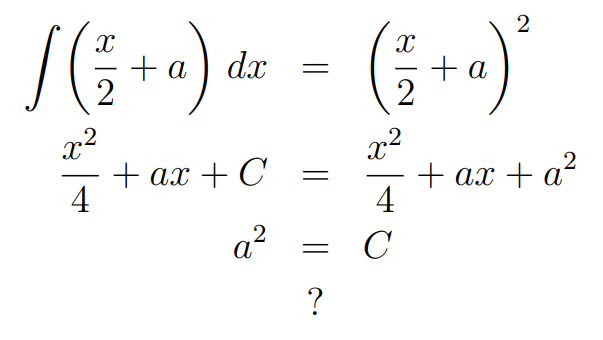
Here, C represents the constant of integration. Thus, for any value of C, the expression x²/4 + ax + C remains an antiderivative of x/2 + a. By setting C equal to a², we find a solution that holds true for any a. This leads us to the somewhat unconventional conclusion that f(x) = x/2 + a for all values of a.

In summary, aside from the final step, we navigated this problem quite smoothly, especially since the f(x)s conveniently canceled out! Stay tuned for a future discussion where I will extend this concept to higher powers of f(x).

Challenge: It's important to note that without initial conditions on differential equations, complications may arise. Can you discover an alternative solution to this problem that doesn't utilize x/2?

Chapter 2: Visual Learning and Integration Techniques

In this video, titled "Integration by completing the square," the concept of completing the square is explored in the context of integration, offering valuable insights into this mathematical technique.

The second video, "Square of Definite Integral," delves into the principles surrounding definite integrals and their squared forms, enhancing understanding of the topic.