Chapter 1: Introduction to the Problem

In this discussion, we aim to identify all positive integer solutions ((a, b, c)) that satisfy the following equation:

frac{a}{2^a} = frac{b}{2^b} + frac{c}{2^c}

This equation presents an interesting mathematical challenge. The question arises: where should one begin to unravel this?

To kick off my approach, I opted to list the values of (frac{a}{2^a}) for small integers (a). It's crucial to remember that we are solely interested in whole number solutions.

Can you identify any triples ((a,b,c)) that satisfy the equation? Simplifying some of the fractions might make this task easier.

The problem does not specify that (a), (b), and (c) need to be distinct. For instance, setting (b) and (c) both equal to 4 yields:

(frac{1}{4} + frac{1}{4} = frac{1}{2})

This implies the solutions ((a, b, c) = (1, 4, 4)) and ((a, b, c) = (2, 4, 4)) are valid.

If you examine the values listed above closely, you may find one additional valid triple. However, I won't reveal it just yet, but I will disclose that this is indeed the only other solution available!

Why is this the case? How can we be certain that no other triples exist further down the list? For example, can (frac{17}{2^n} + frac{19}{2^n}) yield another valid form of (frac{a}{2^a})?

The reason is that (2^n) becomes exceedingly large, making (frac{1}{2^n}) very small. Consequently, (frac{19}{2^n}) remains minor, even when compared to (frac{17}{2^n}) or (frac{18}{2^n}). Thus, the sum (frac{19}{2^n} + frac{18}{2^n}) does not approach (frac{17}{2^n}) in value.

Proof:

It’s evident that (a) must be less than both (b) and (c) for (frac{a}{2^a}) to exceed (frac{b}{2^b}) and (frac{c}{2^c}). The order of (b) and (c) does not affect the equation due to their symmetry.

If (b = c), the equation simplifies to:

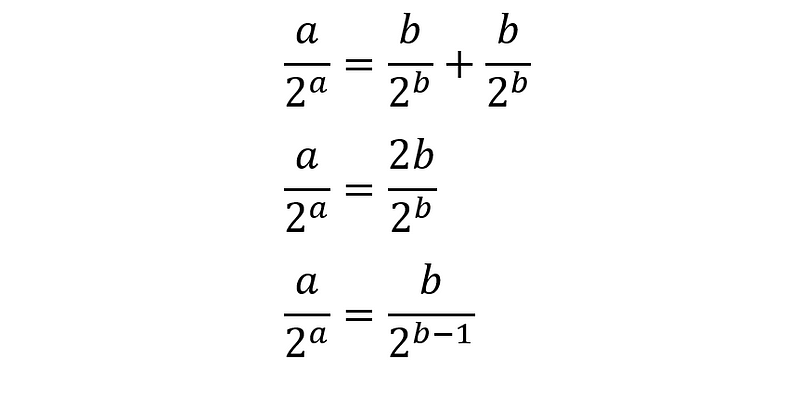
The left side is (frac{a}{2^a}). The numerator must match the exponent in the denominator. It’s impossible for (b) to equal (b - 1), indicating that if a solution exists in this form (which we previously established), it must be in its simplest form.

The only way to simplify a fraction with a power of 2 in the denominator is by dividing by a power of 2.

Dividing by 2 leads to the solution (b = c = 4):

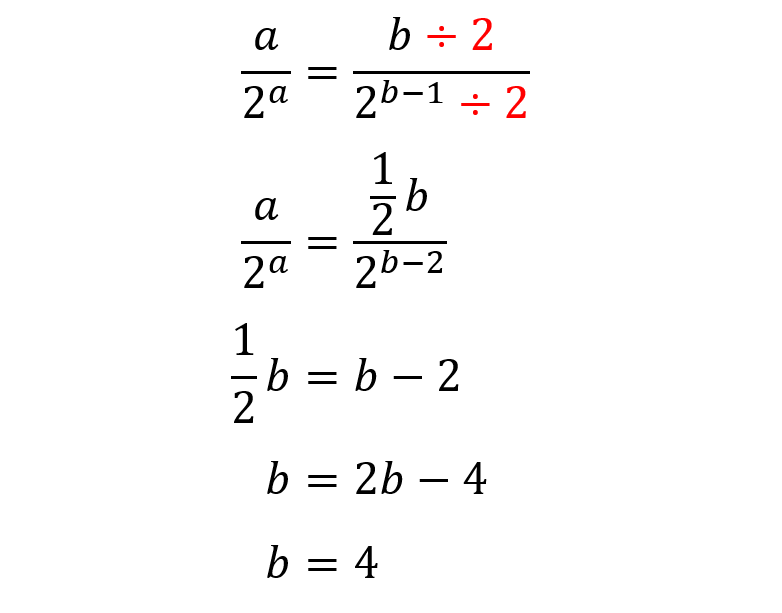
This results in the triples ((a, b, c) = (1, 4, 4)) and ((a, b, c) = (2, 4, 4)).

Examining the next largest power of 2, if we divide by 4 and let (b = c = 8), the equation:

(frac{8}{2^3} + frac{8}{2^3} = frac{8}{2^3})

is slightly greater than (frac{7}{2^3}), yet not nearly as significant as (frac{6}{2^3}), thus failing to yield another solution. The same reasoning applies to larger values of (b).

We can formally demonstrate that no (b > 4) can provide a solution of the form (b = c) since the sum will always fall between the next two larger numbers in the list.

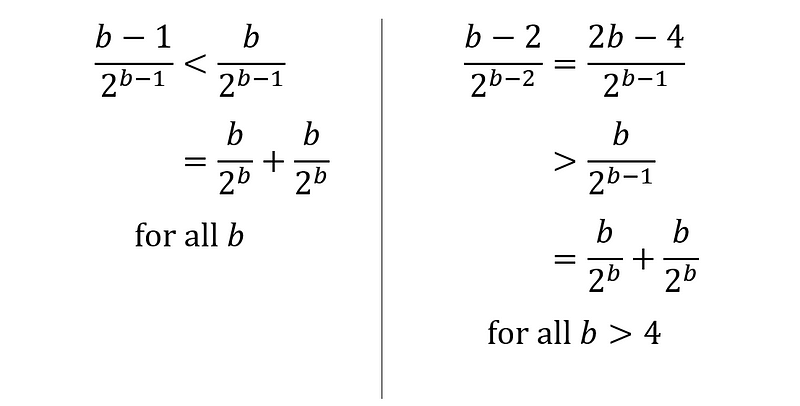
What's next?

What if we let (c = b + 1)? The equation transforms into:

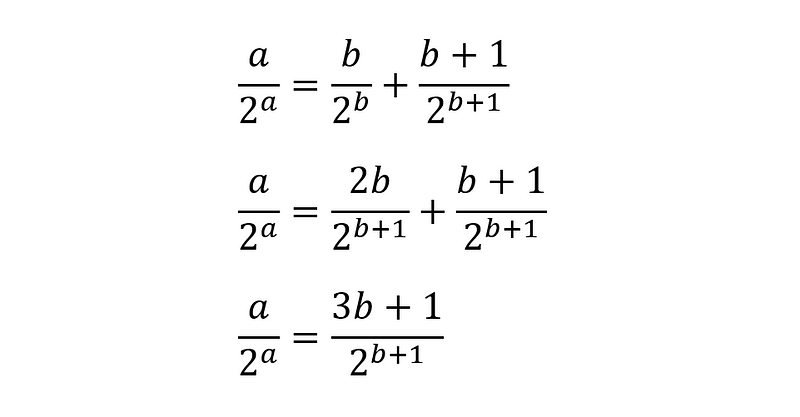
Once again, there are no values of (b) for which (3b + 1 = b + 1). Thus, the fraction must be simplified. Dividing by 2 leads to an invalid (b = -1), but dividing by 4 gives another solution:

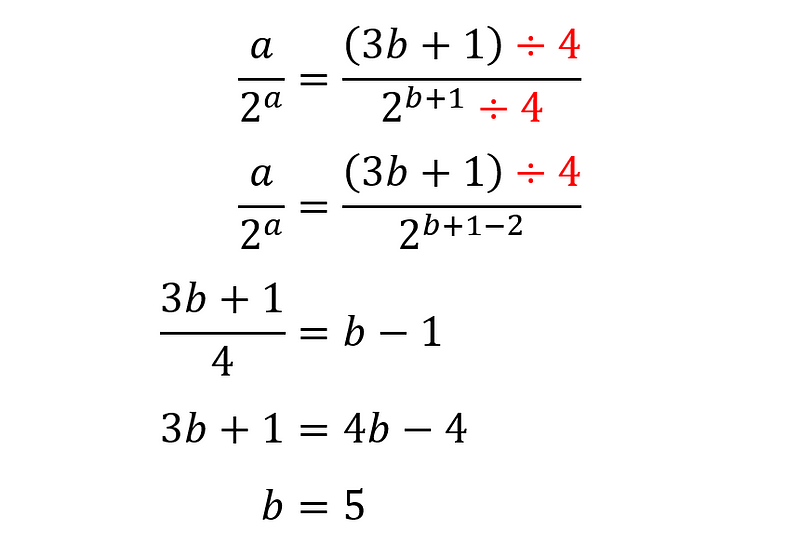
This results in the triple ((a, b, c) = (4, 5, 6)), which happens to be the third and final solution—counting ((a, b, c) = (4, 6, 5)) separately as well.

((a, b, c) = (4, 5, 6))

((a, b, c) = (4, 6, 5))

We can demonstrate that no other solutions of the form (c = b + 1) exist using a similar reasoning as above.

What if we explore (c = b + 2), or even (c = b + 3), etc.? No solutions emerge. The term (frac{2}{2^c}) is too negligible to bring the sum close to the next larger number in the list:

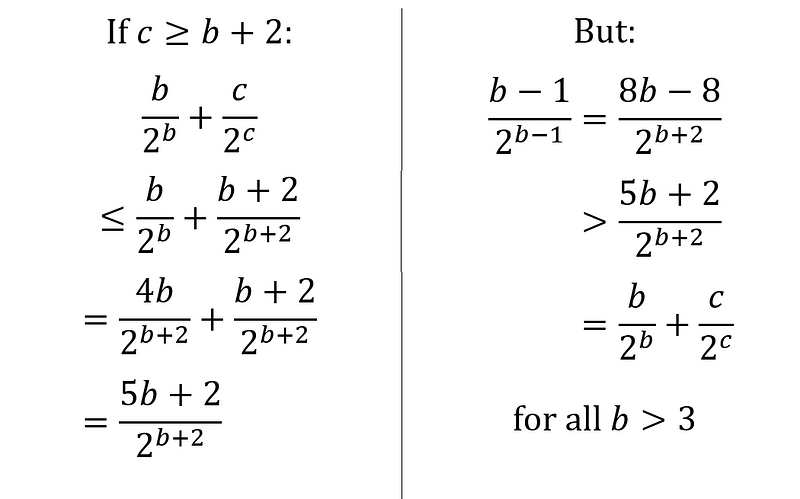
This concludes our search for solutions beyond those already discovered. Here’s a recap of all identified solutions in case you skimmed to the conclusion:

((a, b, c) = (1, 4, 4))

((a, b, c) = (2, 4, 4))

((a, b, c) = (4, 5, 6))

((a, b, c) = (4, 6, 5))

What a fascinating problem! As the first problem in the Chinese Girls Mathematics Olympiad, it serves as an entry-level challenge, yet it remains sufficiently complex to engage even the most enthusiastic problem solvers.