Chapter 1: Understanding Probability and Sums

Throughout my journey in mathematics, I have developed a fondness for probability and statistics. In my early years as a mathematician, I, like many others, leaned towards pure mathematics, often feeling indifferent towards statistics. This sentiment was likely due to my limited exposure to statistical concepts at that time. However, I've recently delved deeper into statistics and have started to appreciate its intricacies.

In this article, I aim to demonstrate how statistics can beautifully intertwine with pure mathematics, revealing fascinating insights. To illustrate this, I will introduce a sum that we will ultimately evaluate together. For any positive integer ( n ), we seek to find the value of the following sum.

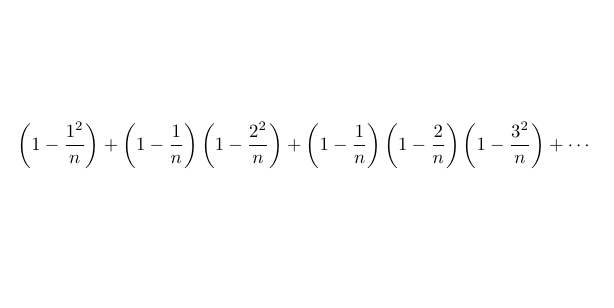
It's important to note that the sum is finite, with the last term being ( (1 - frac{1}{n})... (1 - frac{n^2}{n}) ). By examining small values of ( n ), we might conjecture the value of this sum. However, as mathematicians, our goal is to rigorously prove our conjectures.

Next, let’s consider a scenario that may not initially seem related to the sum we’re evaluating, but we’ll explore it to uncover the connection.

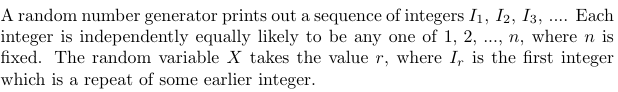
Our first task will be to derive an expression for ( P(X = r) ). This can be accomplished by multiplying the probabilities of each integer up to the ( (r-1) )-th integer being distinct, while the ( r )-th integer is a repeat.

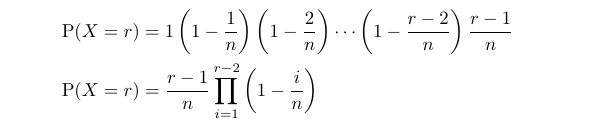
From this expression, we can derive our first sum, utilizing the fact that the total probability sums to 1.

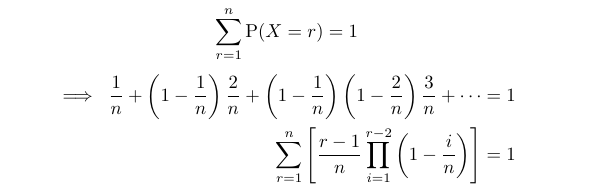
Next, we need to calculate the expectation of ( X ). The expectation of our discrete random variable ( X ) is defined as follows:

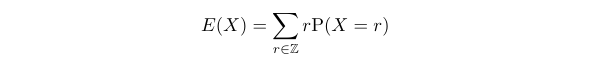
Let us proceed to compute the expectation of ( X ) in this context.

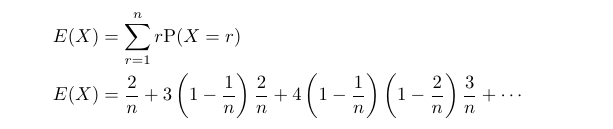
Some readers may notice that the expressions and sums we are generating resemble those of our target sum. Let’s move forward! We’ll recall an alternative method for expressing the expectation of a discrete variable ( X ) that takes values from 1 to ( n ).

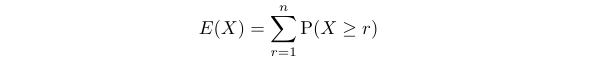
To utilize this, we must find an expression for ( P(X leq r) ), which can be determined by calculating the probability that the first ( r-1 ) integers are distinct.

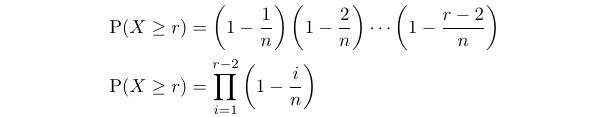
Observe that ( P(X leq 1) = P(X leq 2) = 1 ). We can substitute this into the equation involving the expectation of ( X ).

The final and enlightening step is to merge the two sums we've derived to arrive at the final sum and its value. This leads us to the following two equations.

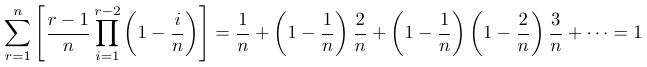
Equation 1

Equation 2

The summations are presented in both product and sum forms for clarity, illustrating how we can extract the squared term in our desired sum.

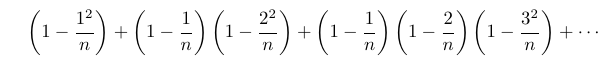
By subtracting equation 1 from equation 2, we can observe the emergence of the squared terms.

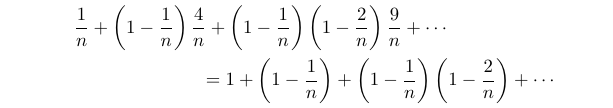
Finally, we can rearrange everything to one side to achieve the following result.

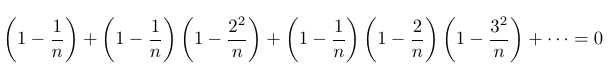
What a delightful outcome! I hope you found this exploration of using probability to calculate sums as intriguing as I did.

Thank you for reading! If you have any insights or thoughts on the development of this solution, please feel free to share.

Chapter 2: Video Resources for Deeper Understanding

In this video, titled "Determine Sample Sum Probabilities Using the TI-84," viewers can learn how to utilize the TI-84 calculator to compute sample sum probabilities effectively.

The second video, "All Probabilities Sum to 1," provides a concise explanation of the fundamental concept that all probabilities within a probability space must sum to one.