Chapter 1: The Historical Context of Pythagoras's Theorem

What makes quadratic forms and "geometric algebras" so crucial in contemporary physics and the mathematics of the early 20th century? To understand this, we must acknowledge the ancient wisdom from cultures such as India and Mesopotamia.

The theorem often associated with the Greek philosopher, ascetic, and cult figure Pythagoras of Samos is, in reality, rooted in traditions far older. Ancient Hindu texts, specifically the Baudhayana Shulba-Sutras and the Apastamba Shulba Sutras, illustrate that the construction of Hindu ritual sites already embraced the Pythagorean Theorem by at least the middle of the first millennium BCE. This theorem was also recognized in ancient China, possibly as early as 1100 BCE, and historians in Mesopotamia suggest that it was well understood by craftsmen and philosophers during the Old Babylonian era, spanning from 2000 BCE to 1600 BCE.

The pervasive nature of this theorem in geometry and our understanding of the world implies that cultures reflecting on their surroundings with reverence and curiosity would naturally arrive at these insights. Evidence of awareness of Pythagoras’s Theorem can be found in numerous ancient civilizations: Nigeria, China, Mesopotamia, Egypt, and India.

As we will explore, Pythagoras's Theorem correlates with a summation rule for areas. When considering Euclid's first four postulates as axioms, the theorem can be seen as equivalent to the fifth postulate; thus, the fifth postulate implies Pythagoras and vice versa. Modern geometry increasingly relies on variations of Pythagoras's Theorem as foundational principles, as they align more closely with contemporary algebraic methods. Pythagoras's Theorem is a quadratic form, a topic of considerable study in the 19th century, notably by Hermann Minkowski, a mentor to Albert Einstein.

The first video, "Esoteric Corner: Pythagorean Numerology - Its Form and Legacy," delves into the historical context and significance of Pythagorean numerology, highlighting its impact on our understanding of mathematics.

Chapter 2: The Nature of Geometry and Its Foundations

What is all the excitement surrounding a seemingly simple algebraic form? The answer lies in the profound connections between Pythagoras's Theorem, its generalizations, and our fundamental concepts of distance and area, which I aim to elucidate in this article and those that follow.

Let's traverse the journey from Ancient India to Plato's Greece and onward to 19th Century Göttingen. James Abram Garfield, primarily known as the 20th President of the United States and a notable abolitionist, also authored an elegant and modern proof of Pythagoras's Theorem. His proof, often overlooked, emphasizes the concept of shear mapping and area invariance under these transformations.

The second video, "Pythagoras to Plato: The Ancient Greek Revolution in Human Thought," explores the evolution of philosophical thought from Pythagoras to Plato, shedding light on the development of mathematical concepts.

Garfield's proof is particularly intriguing because shear and squeeze mappings—such as those found in the Lorentz Transformation of Special Relativity—are not Euclidean isometries, yet they preserve area. This hints at a deeper geometric understanding tied to Pythagoras's Theorem.

Section 2.1: The Additivity of Areas and Basic Measurement Concepts

I first learned to prove Pythagoras's Theorem in 1977, utilizing an algebraic approach that hinges on the conservation of area—no matter how an area is divided, the total area remains constant. This area summation property is foundational to modern measure theory and integration, encapsulated in the countable additivity axiom.

In Garfield's time, similar to Euclid's era, concepts of area and angle were intuitive, and the additive property of measure is subtly embedded in Euclid's own proof of the theorem. While Euclid’s proof is beautifully constructed, it relies on notions not directly included in his axioms, such as the additivity of measures and the invariance of areas under transformations, which he did not explicitly axiomatize.

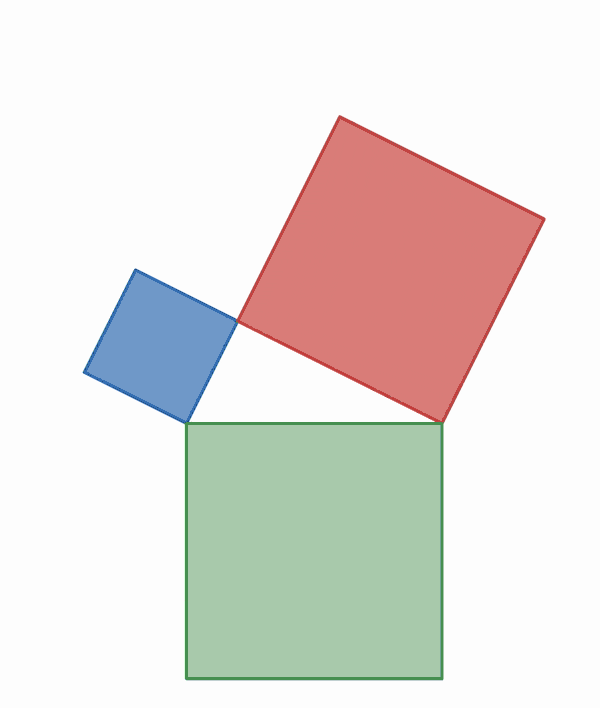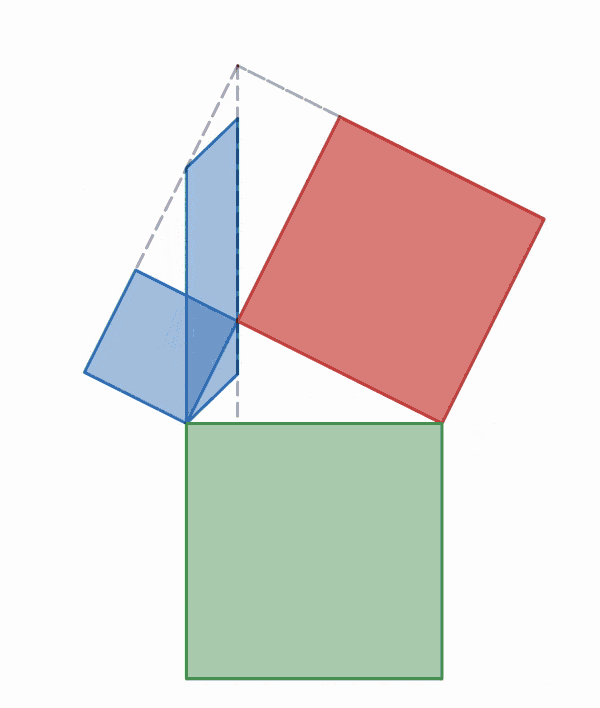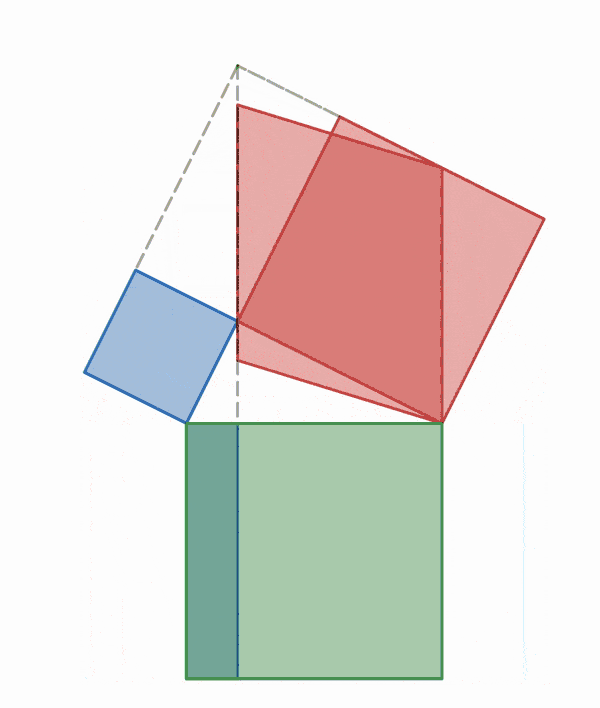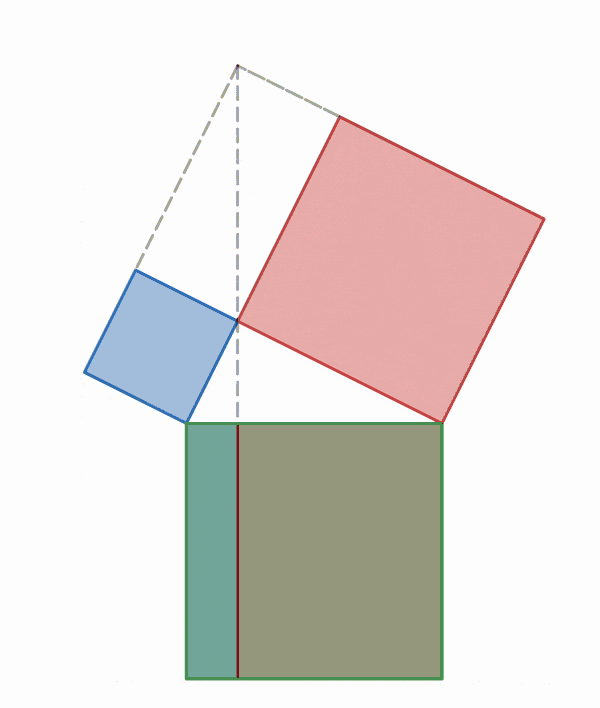
A graphical illustration displaying the central ideas of Garfield's proof—the invariance of area under shear mapping and the additive property of areas.