Understanding Compactification Theorems in Topology
Written on
Chapter 1: An Introduction to Compact Spaces
If you haven't delved into topology, the term "compact space" might be unfamiliar to you. Essentially, compact spaces possess numerous beneficial characteristics.
In the early 20th century, mathematicians sought to extend essential theorems from calculus, such as the Extreme Value Theorem (which states that continuous functions on closed intervals achieve maximum and minimum values), to broader contexts. Compact spaces frequently dominate initial topology courses; hence, we won't cover every nuance here. The crucial takeaway is that many theorems concerning compact spaces exist, and these spaces are generally more manageable to work with.
However, the majority of spaces are not compact, prompting the development of various theorems that explore how to "compactify" non-compact spaces and which properties remain intact post-compactification. More details on this will follow in later sections.
Section 1.1: Defining Compact Spaces
The formal definition of compact spaces can be quite abstract, often leaving readers puzzled. For clarity, we propose a practical definition: a space (X) is compact if every infinite collection of points must converge at some location within that space. In simpler terms, if you attempt to distribute infinitely many points, they will inevitably cluster together.
This perspective aligns well with the term "compact." Consider a few illustrations.
The real number line exemplifies a non-compact space, as you can distribute an infinite number of points along the integers.
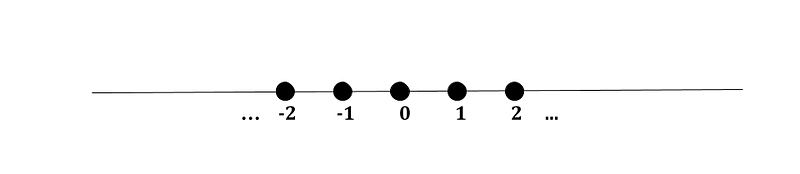
In contrast, a closed finite interval, including its endpoints, is compact. It's intuitively clear that if you attempt to place infinitely many points within a finite space, they will converge somewhere. Although proving this notion requires a more rigorous understanding of "accumulation points," the intuition holds.
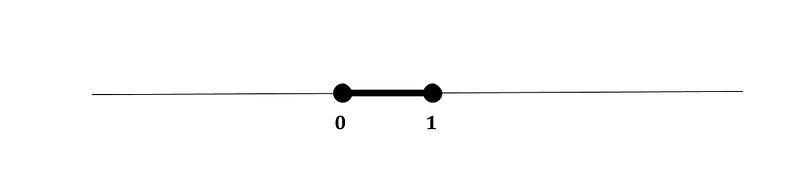
On the flip side, an open interval, such as (0,1), is not compact. The sequence generated by (1/n) (for (n geq 2)) converges to 0, which is not included in this space.

This highlights the distinction between closed and open intervals in terms of compactness.
Section 1.2: Characteristics of Compact Spaces
When dealing with spaces formed from the traditional real number system, compact spaces are easy to classify: they are precisely the closed and bounded subsets.
"Bounded" implies that the entire set can fit within a large sphere, making it evident why boundedness is crucial for compactness. If a subset extends infinitely, points can be spread out without clustering. The concept of "closed" is a more nuanced topological idea, indicating that any accumulation point of the set is also contained within it.
When using these definitions, it becomes apparent that compact spaces can be categorized as closed and bounded. However, remember that these definitions may not align perfectly with textbook definitions.
In many practical applications, spaces may not arise from merely selecting subsets from (mathbb{R}).
This video, titled "Compactifications," further elaborates on compact spaces and their properties.
Section 1.3: Compactification Techniques
Most spaces are not compact, leading to inquiries about how to embed these spaces within compact ones. This process is known as compactification.
Subsection 1.3.1: One-Point Compactification
A straightforward method of compactification is the one-point compactification. This technique involves adding a single point to a space, thus transforming it into a compact space.
For instance, consider the real number line, which is non-compact due to its infinite extension. By introducing a point at infinity, we can visualize this by wrapping the number line around a circle.

This idea can be formalized through stereographic projection. When a line is drawn from the top of the circle to intersect it, every point of (mathbb{R}) is covered once, with the additional point representing infinity.
The concept of one-point compactification, while minimalistic, has some limitations, especially concerning the peculiarities of certain topological spaces.
Subsection 1.3.2: Stone-?ech Compactification
The Stone-?ech compactification, first articulated by Eduard ?ech in 1937 and later refined by Marshall Stone, represents a more complex yet ingenious method of compactification.
A key preliminary concept is that the product of two compact spaces remains compact, a fact that, while straightforward to prove, is fundamental.
For example, while (mathbb{R}^2) is not compact due to its unbounded nature, the closed interval ([0,1]) is compact. When combined in a product to form ([0,1]^2), we generate a solid, closed square, with ([0,1]^3) yielding a solid cube.
A remarkable theorem, known as the Tychonoff Theorem, asserts that any arbitrary product of compact spaces is also compact.
This theorem is non-trivial to prove, despite its seemingly evident nature. By cleverly locating a copy of a space (X) within an expansive product of ([0,1]) (over an uncountably infinite set) and then taking the closure of (X), we ascertain that the outcome is compact.
You may wonder about the practicality of this approach compared to one-point compactification; however, it possesses a significant advantage: it is a "universal" construction. Essentially, every other compactification method can be viewed as a subset of the Stone-?ech compactification.
With an understanding of both minimal and maximal compactifications, we can appreciate the nature of compact spaces and the processes that yield them.
The video titled "Compactification of a topological space" provides further insight into the compactification techniques discussed.