Chapter 1: What Are Integrals?

Integral calculus focuses on calculating integrals, which can be viewed as anti-derivatives—essentially the reverse process of differentiating a function. More broadly, integrals symbolize measurable values, such as the area beneath a curve. For example, consider the area below the curve of x² and above the x-axis between two points, x = a and x = b:

While many functions can be integrated precisely, a fundamental concept of a definite integral involves starting from simple rectangular regions with finite width, denoted as Δx, and height f(x), as illustrated in Figure 1:

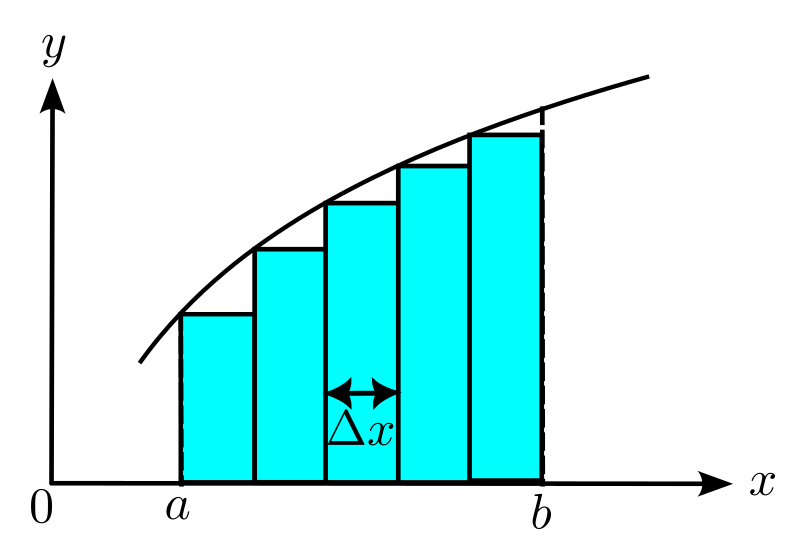
The principle is that by increasing the number of rectangles with narrower widths, we achieve a more precise approximation of the actual area, as depicted in Figure 2:

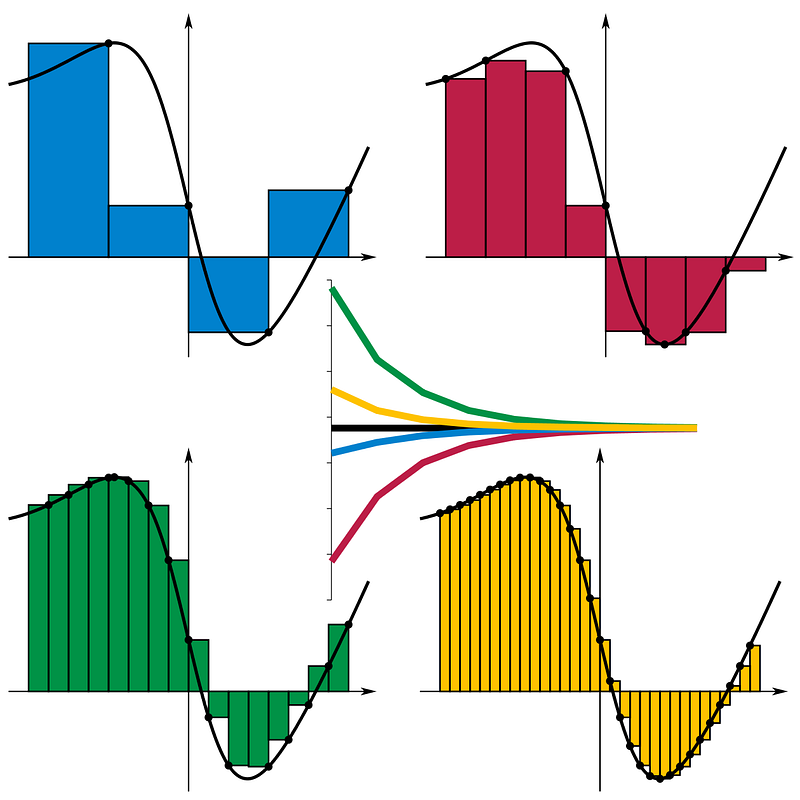
Thus, the area (integral) can be expressed as the summation of all these rectangles in the limit as the number of rectangles approaches infinity, known as a Riemann sum:

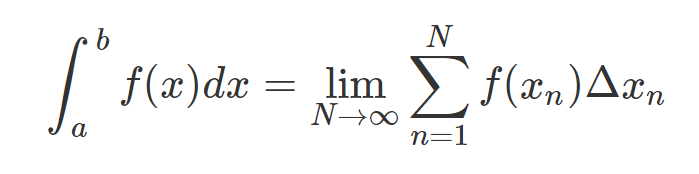
In a specific case where all rectangle widths are equal, we can formulate:

It's essential to note that with N subdivisions between points a and b (inclusive), there will be N-1 rectangles. To illustrate, let's analyze the following integral:

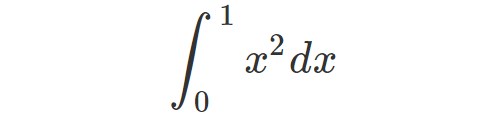
According to calculus principles, we can use the antiderivative of x², which is x³/3, to calculate:

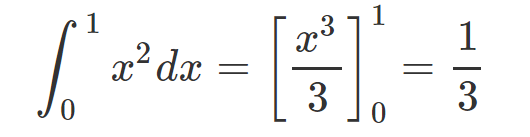
However, if we are unfamiliar with this formula or seek a more rigorous validation, we can apply the Riemann sum method to substantiate the result:

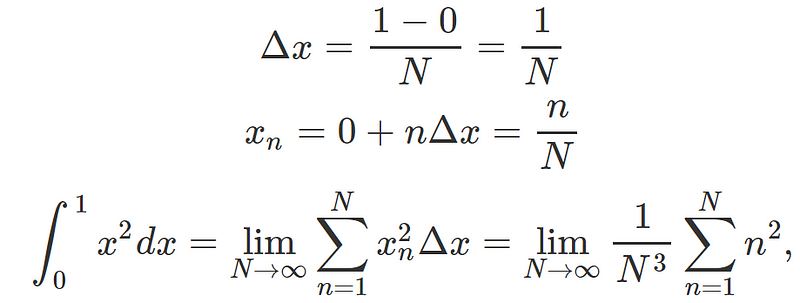
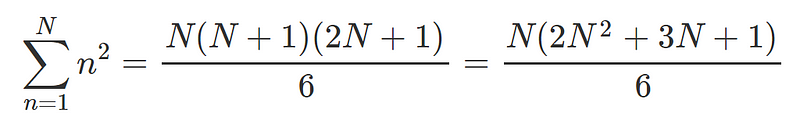
In this case, we ultimately obtain:

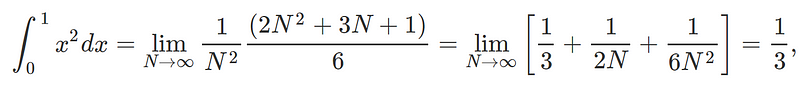
It is important to understand that the definition of a definite integral via Riemann sums is applicable to various kinds of smooth continuous functions.

This video introduces the concept of integrals and their significance in mathematics.

Chapter 2: Visualizing Integrals

A detailed explanation of integrals, their applications, and examples.