Chapter 1: Introduction to Time Crystals

In August, Google released a preprint on ArXiv revealing their achievement of creating a time crystal using a quantum computer. The term "time crystal" may sound like a concept from a science fiction film—something I personally find fascinating, especially in animated shows like Rick and Morty. This article aims to clarify the essence of this groundbreaking concept.

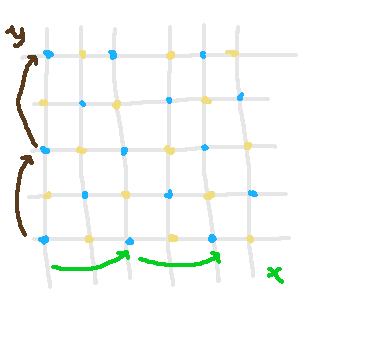
To begin, let's clarify the traditional definition of a crystal. A crystal structure exhibits discrete translational symmetry rather than continuous symmetry. Picture a material where atoms are arranged in an infinitely extending square grid, with each square measuring 1 unit in length. This arrangement is classified as a crystal, as translations along the x or y axes do not maintain the grid's invariance at distances less than 1 unit. In simpler terms, it lacks continuous symmetry and instead possesses discrete symmetry. A time crystal operates similarly, breaking translational symmetry, but in the dimension of time.

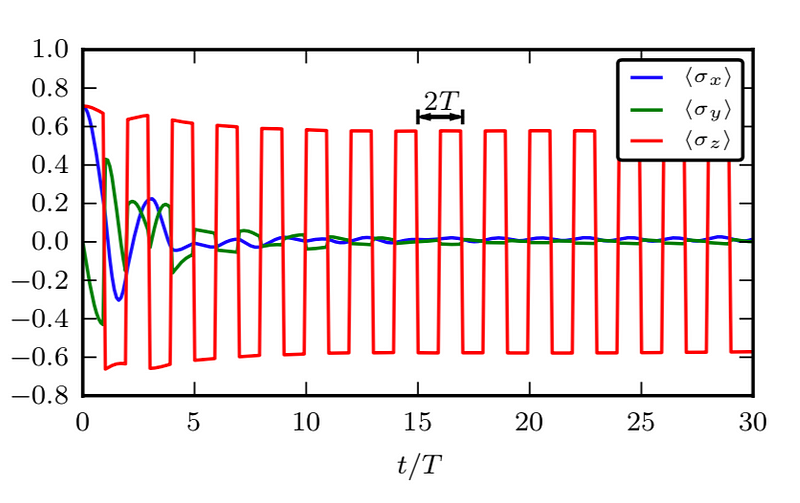
The physical interpretation of a system that lacks time translation symmetry is that it is in a state of perpetual motion. When discussing quantum systems, it is essential to refer to quantum states. Here, we seek a ground state, characterized by minimal energy, which evolves over time. This state exhibits continuous movement, akin to a perpetual motion machine. The accompanying diagram illustrates values of three spin observables within a Floquet system that possesses time translation symmetry, represented as t ? t + T. The y-axis indicates average spin values, while the three lines correspond to average spins along the x, y, and z axes. Notably, these observables disrupt time translation symmetry as their values do not maintain a periodicity of T.

Chapter 2: Time-Translation Symmetry and Its Implications

In the realm of quantum mechanics, the physical system is characterized by its Hamiltonian, an operator that signifies the system's energy. Generally, a Hamiltonian remains unchanged after a transformation, which indicates a symmetry. However, ground states—defined as the lowest energy states permissible in a quantum system—might not share the same symmetries as the Hamiltonian itself. This discrepancy is termed symmetry breaking.

As discussed in a prior article, the Ising model serves as a straightforward illustration of symmetry breaking. In this model, an arrangement of atoms is either in an up-spin or down-spin state. While the Hamiltonian maintains invariance during the transformation between up and down spins, the minimal energy states exist solely as either all up or all down, thereby breaking the symmetry. Nonetheless, alternative ground states that do conform to this symmetry exist, known as cat states, which exhibit a high degree of entanglement.

In quantum computing, these states are referred to as Greenberger–Horne–Zeilinger (GHZ) states. This state represents a superposition of configurations with all spins up and all spins down. It holds equivalent energy to either ground state, making it a ground state in its own right. However, this state is considered "long-range correlated," indicating a significant level of entanglement. Such entanglement implies that the atoms in this arrangement exhibit correlations during repeated measurements. In practical terms, this high degree of entanglement poses a risk of quantum decoherence when interacting with the environment, making these states unfeasible for large atom collections.

Symmetry breaking is a crucial concept in physics, particularly with time-translation symmetry. This type of symmetry occurs when the Hamiltonian's time can be shifted by a certain amount without altering its appearance. For a quantum state, having time-translation symmetry means that as the state evolves over time, it retains the same characteristics. A state with short-range correlations exhibits a lack of correlation between local operators at increasing distances.

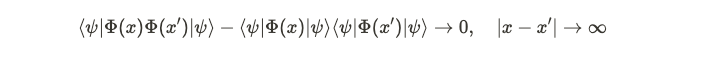
Chapter 3: The Nature of Time-Translation Asymmetry

The equation below illustrates this concept, where H represents the Hamiltonian, and psi denotes an observable state. Typically, a ground state is identified as one with the lowest, defined energy. For a system to exhibit definite energy, it must be an eigenstate of the Hamiltonian. However, if it were indeed an eigenstate, the expected value of the state should not fluctuate over time.

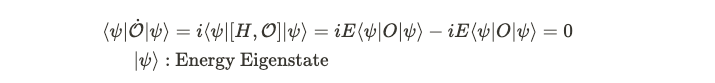
The equation shows O as an operator, which can signify any observable property, such as total angular momentum or momentum in a specific direction. The left side reflects the expected value of the change in this observable. Transitioning from the first term to the next involves Heisenberg’s equation, which describes how an operator evolves. The fact that time evolution approaches zero implies that the expected value of the operator in this state remains unchanged. Therefore, time-translation asymmetry appears to be implausible, as our observables remain constant over time.

Chapter 4: Exploring Floquet Time Crystals

To circumvent this apparent impossibility, we need to increase the system's size, allowing for a more extended period to reach a stable equilibrium state. The observations noted above encourage a more precise interpretation of time-translation symmetry. In the referenced paper, the authors outline two equivalent definitions for time translation symmetry breaking, based on a Hamiltonian exhibiting discrete-time symmetry.

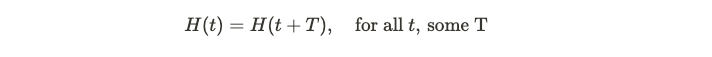
According to one definition, time translation symmetry breaking occurs when the expected value of any observable in a time-translated state diverges from the original expected value. In this scenario, the Hamiltonian maintains time translation symmetry concerning period T, while the state itself does not.

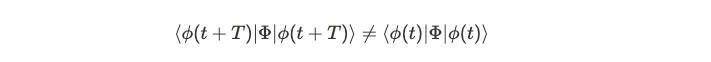
The first video titled "BREAKING: New Phase of Matter" explores the concept of time crystals and their implications in quantum physics, offering insights into this fascinating subject.

The second video titled "What Does a Real Time Crystal Look Like?" provides a visual representation of time crystals and their properties, making the concept more accessible to viewers.

References

[1] F. Wilczek, Phys. Rev. Lett. 109, 160401 (2012), arXiv:1202.2539 [quant-ph].

[2] arXiv:2107.13571 [quant-ph]

[4] Dominic V. Else, Bela Bauer, and Chetan Nayak. Floquet Time Crystals